Playing Atari with Deep Reinforcement Learning

Date: 2016-11-27 22:30:00, GMT+8
Speaker: zlslhp
References:
https://arxiv.org/abs/1312.5602

Playing Atari with Deep Reinforcement Learning

Background

Could AI learn to control itself with the raw input from the environment, rather than receiving the hand-crafted features. In this article, the authors introduced an approach which combines reinforcement learning and deep neural network. This new deep learning model demonstrates its ability to master different control policies for different Atari 2600 games with only raw pixel input.

Reinforcement Learning

Future reward and its Bellman’s expression: $R_{t}=\sum_{ {t}'=t}^{T }\gamma ^{ {t'}-t}r_{ {t}'}=r+\gamma R_{t^{'} }$

The optimal action-value function: $Q^{*}(s,a)=max_{\pi } \mathbb{E}[R_{t}|s_{t}=s,a_{t}=a,\pi]$ This means the maximum expected return achievable, after seeing some sequence $s$ and then taking some action $a$ and by following policy $\pi$, which mapping sequence to actions.

The $Q^{}(s,a)$ could be expressed using Bellman’s equation: $Q^{*}(s,a)=\mathbb{E}_{s^{'}\sim \varepsilon }[r+\gamma max_{ {a}'}Q^{*}({s}',{a}')|s,a]$ However, $Q^{}(s,a)$ is an optimal value. Normally, people use using the Bellman equation $Q_{i+1}(s,a)=\mathbb{E}[r+\gamma max_{ {a}'}Q_{i}({s}',{a}')|s,a]$ as an iterative update to converge to the optimal action-value function, when $Q_{i}\rightarrow Q^{*} $ as $i \rightarrow \infty $.

In this article, a neural network is used as a non-linear approximator to estimate the action-value function, $Q(s,a;\theta )\approx Q^{*}(s,a)$, where $\theta$ stands for the weights. The loss function could be decribed as follows: $L_{i}(\theta_{i})=\mathbb{E}_{s,a\sim \rho (\cdot)}[(y_{i}-Q(s,a;\theta_{i}))^{2}]$ , where $y_{i}=\mathbb{E}{ {s}’\sim \varepsilon }[r+\gamma max{ {a}’}Q_{i}({s}’,{a}’;\theta_{i-1})|s,a]$ and $\rho(s,a)$ is a probability distribution over sequences $s$ and actions $a$.

$\epsilon $-greedy

The next action is selected using $\epsilon $-greedy strategy. $\begin{cases} a=\underset{a\in A}{max}Q^{*}(s,a)& \text{with probability }1-\epsilon \\ \text{random action}& \text{with probability }\epsilon \end{cases}$

Algorithm

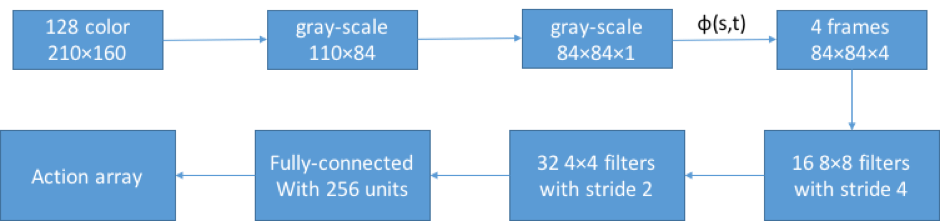
Architecture

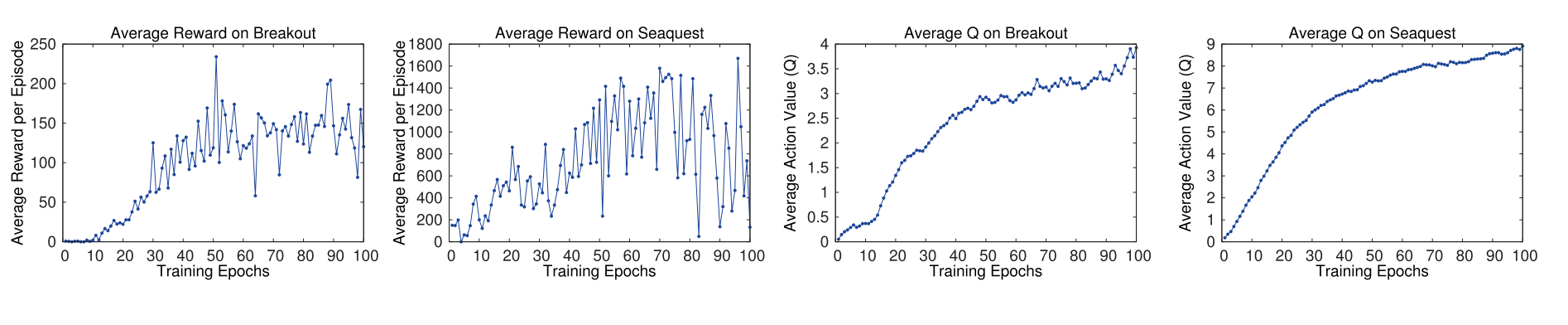
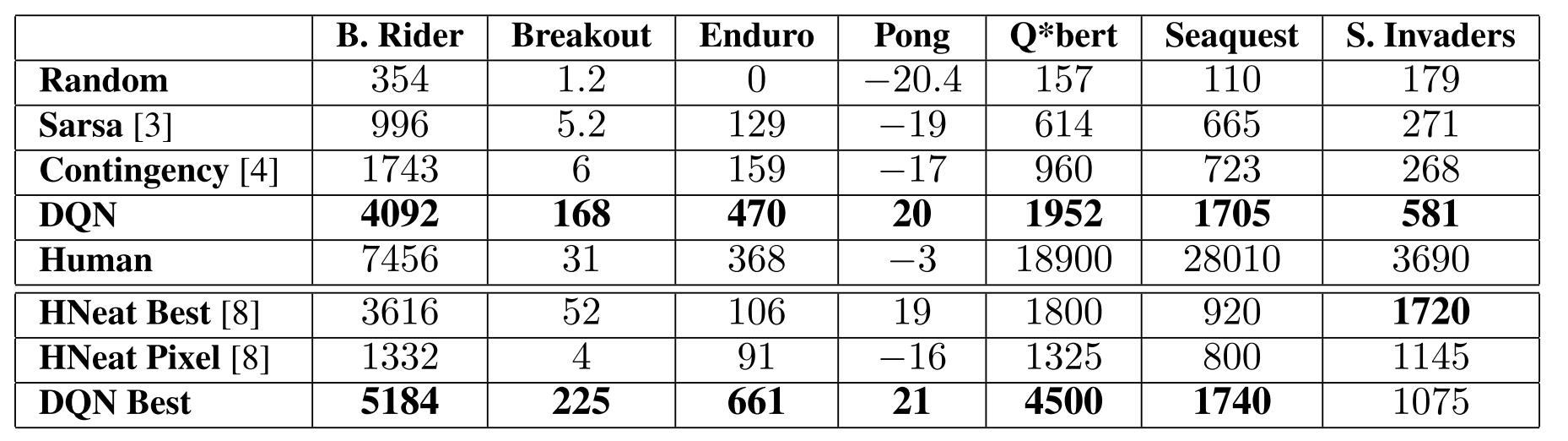
Experiment and Results

The two plots on the left show average reward per episode on Breakout and Seaquest respectively during training. The statistics were computed by running an $\epsilon$-greedy policy with $\epsilon$ = 0.05 for 10000 steps. The two plots on the right show the average maximum predicted action-value of a held out set of states on Breakout and Seaquest respectively. One epoch corresponds to 50000 minibatch weight updates or roughly 30 minutes of training time.

The leftmost plot shows the predicted value function for a 30 frame segment of the game Seaquest. The three screenshots correspond to the frames labeled by A, B, and C respectively.

The upper table compares average total reward for various learning methods by running an $\epsilon$-greedy policy with $\epsilon =0.05$ for a fixed number of steps. The lower table reports results of the single best performing episode for HNeat and DQN. HNeat produces deterministic policies that always get the same score while DQN used an $\epsilon$-greedy policy with $\epsilon =0.05$.

*****

Explore other reading clubs